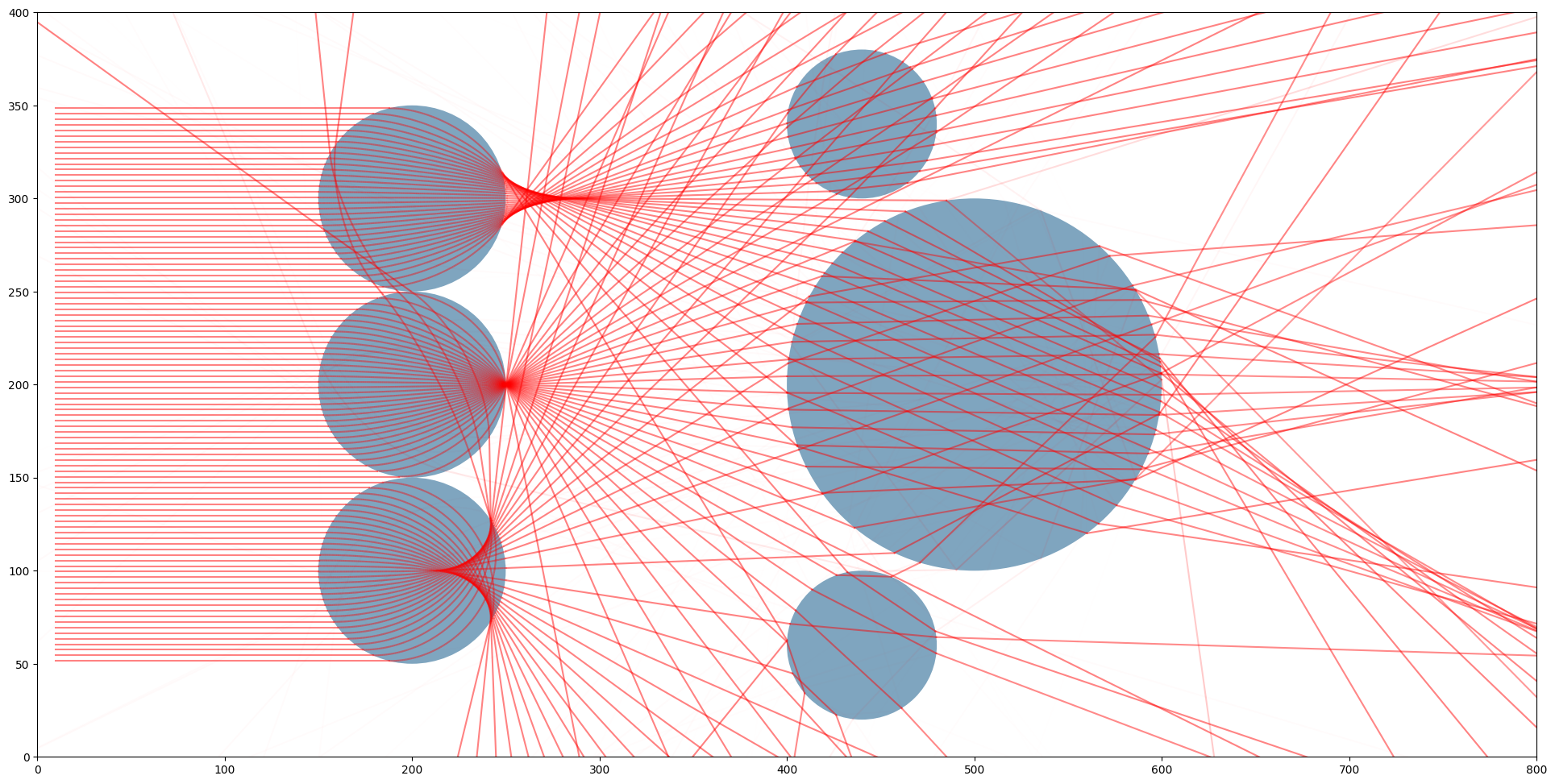
This was the final project for a Computational Optics seminar completed in collaboration with Claire Paré. Made in a jupyter notebook with numpy and matplotlib, the first aim of this project was to create a simplified version of this 2D ray-optics simulator. The initial goal was to show the paths of light rays through transparent spheres with various indices of refraction and accurately model Fresnel effects to showcase how the amount of reflected and refracted light depends on the index of refraction and incoming ray angle. Next, we implemented continuous refraction, showcasing the bent paths light rays take as they travel through objects with spatially varying refractive indices. Our implementation of this was based off the paper Path Tracing Estimators for Refractive Radiative Transfer by Pediredle et. al., from whom we also got the idea of modelling Luneberg lenses.
Part of this project was also a presentation in which we talked about the basics of ray tracing and covered the research paper mentioned above in more detail. The code we wrote for the project was meant to showcase a part of the work shown in that paper in a more approachable and educational manner. As such, the notebook also features explanations on how ray tracing works and the particulars of our implementation of it.
The colab notebook for this project can be accessed here.
Other Renders
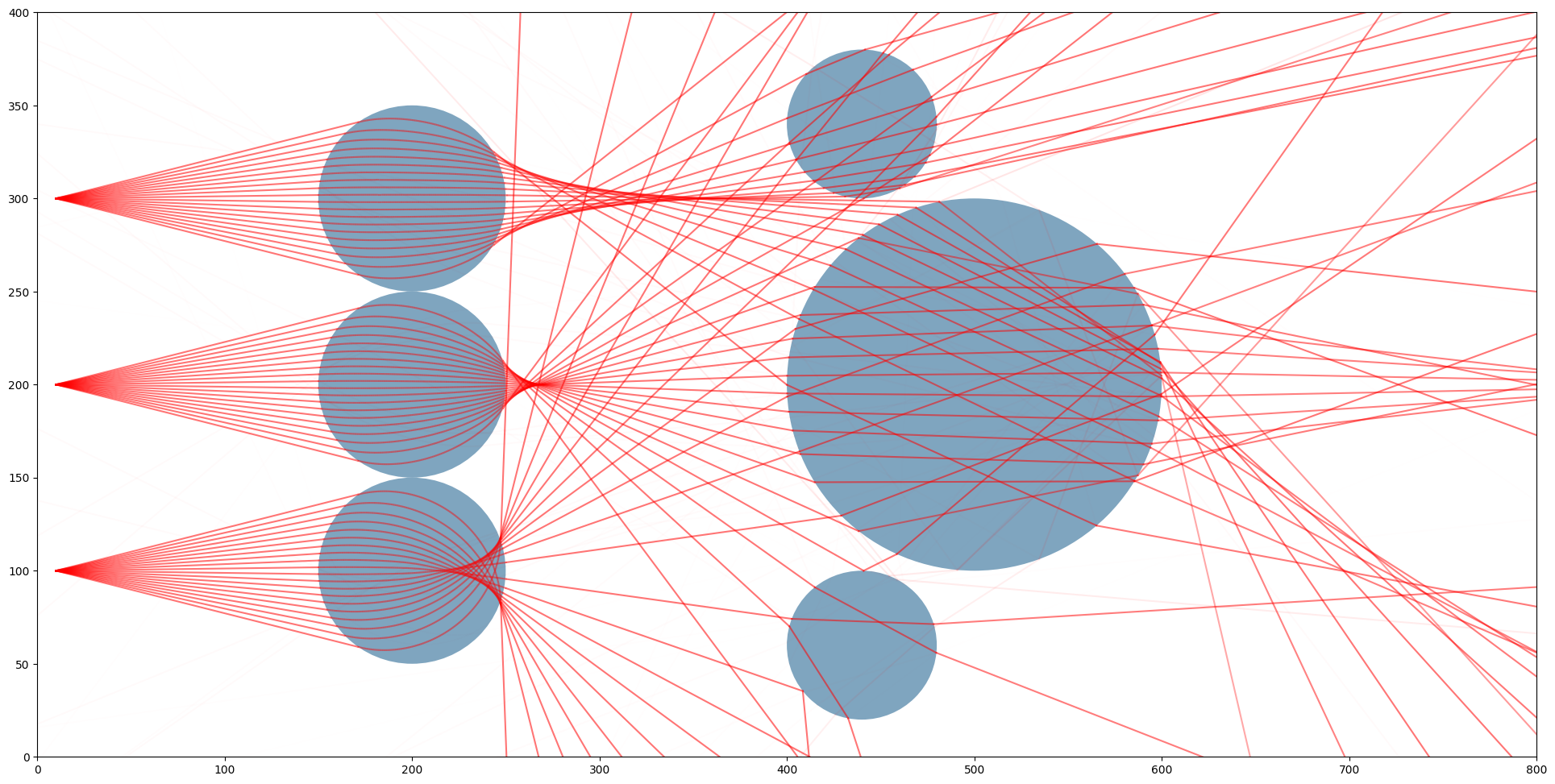The same scene as the image above but with three spotlight sources going into each Luneburg lens.
A scene featuring three circles with different indices of refraction (top: 1.05, middle: 1.5, bottom: 0.7) showcasing their various foci and spherical abberations.
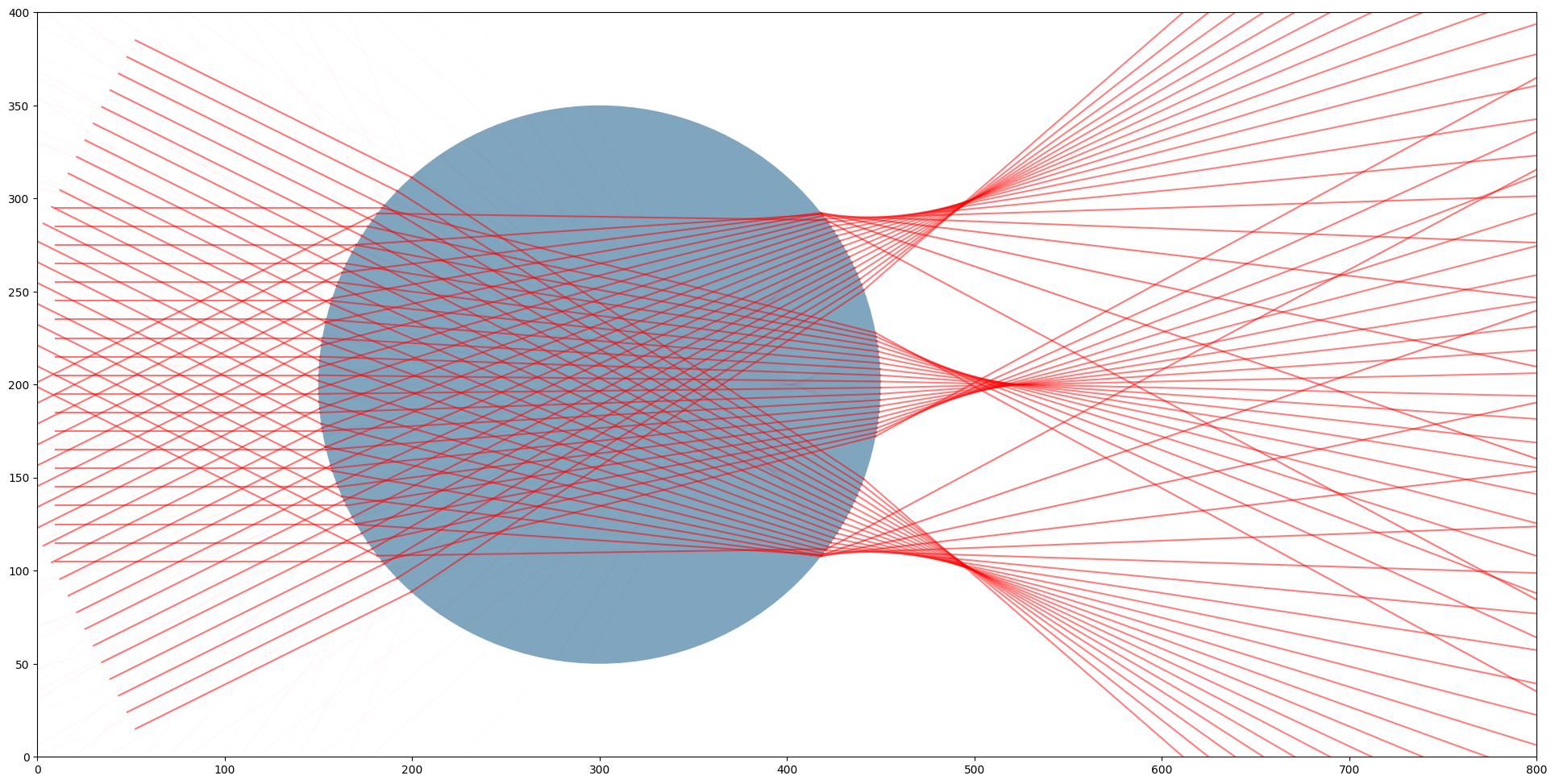Parallel rays going into a single large circle with an index of refraction of 1.5 from different directions, showcasing how the abberations change according to incoming ray directions.
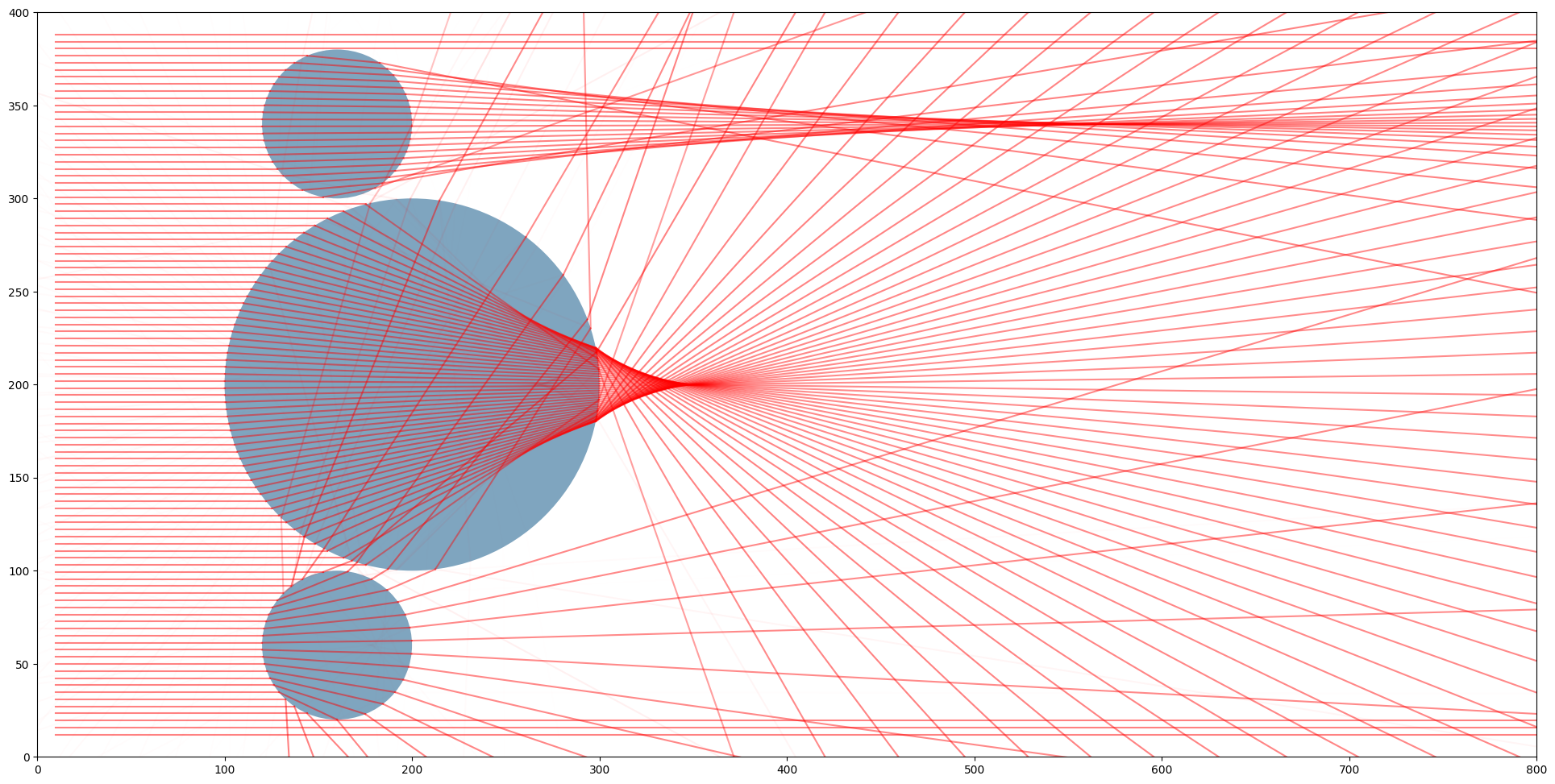
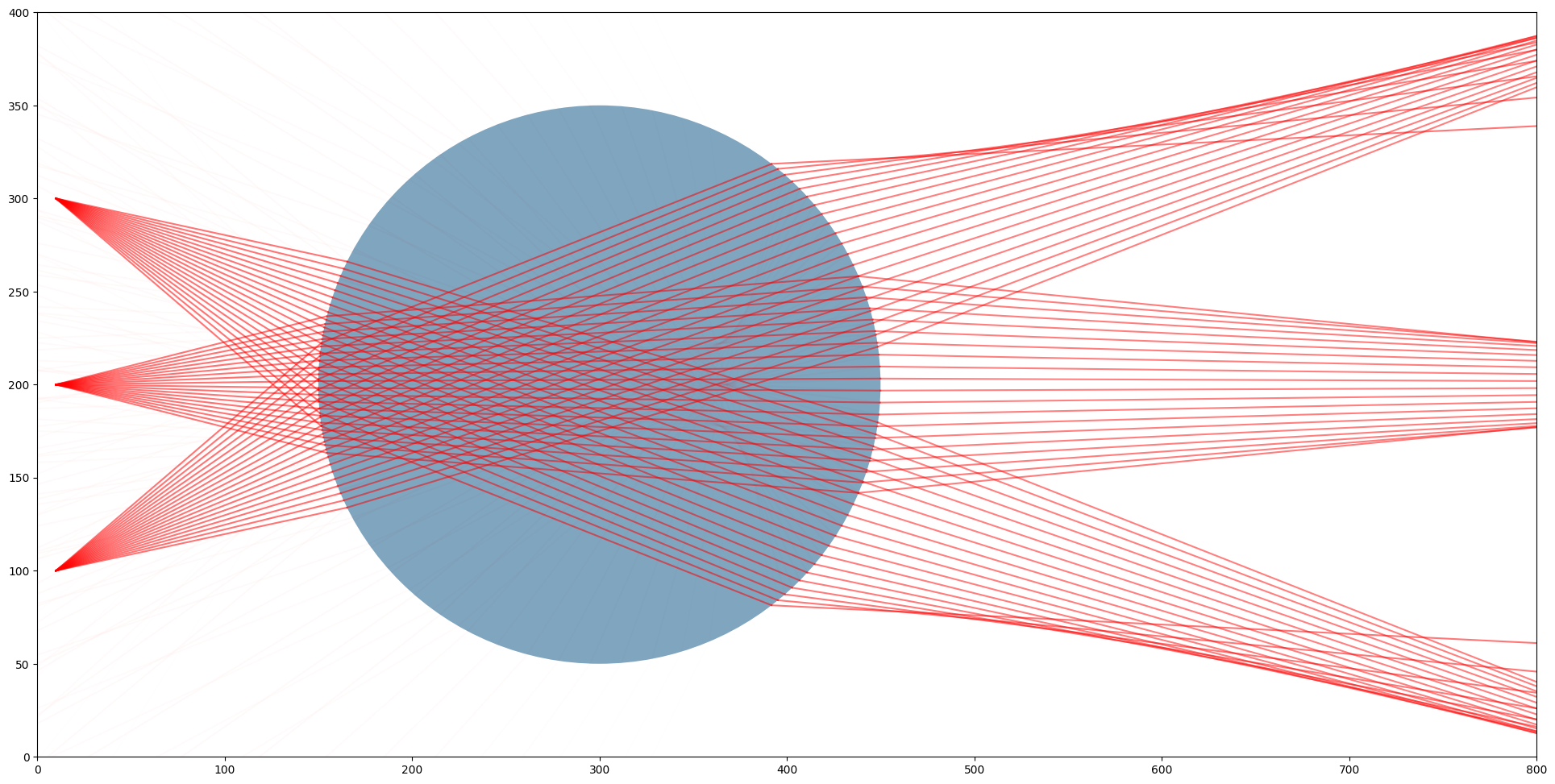The same scene as above but now with spot light sources, showcasing how the focus for not parallel rays is much farther.
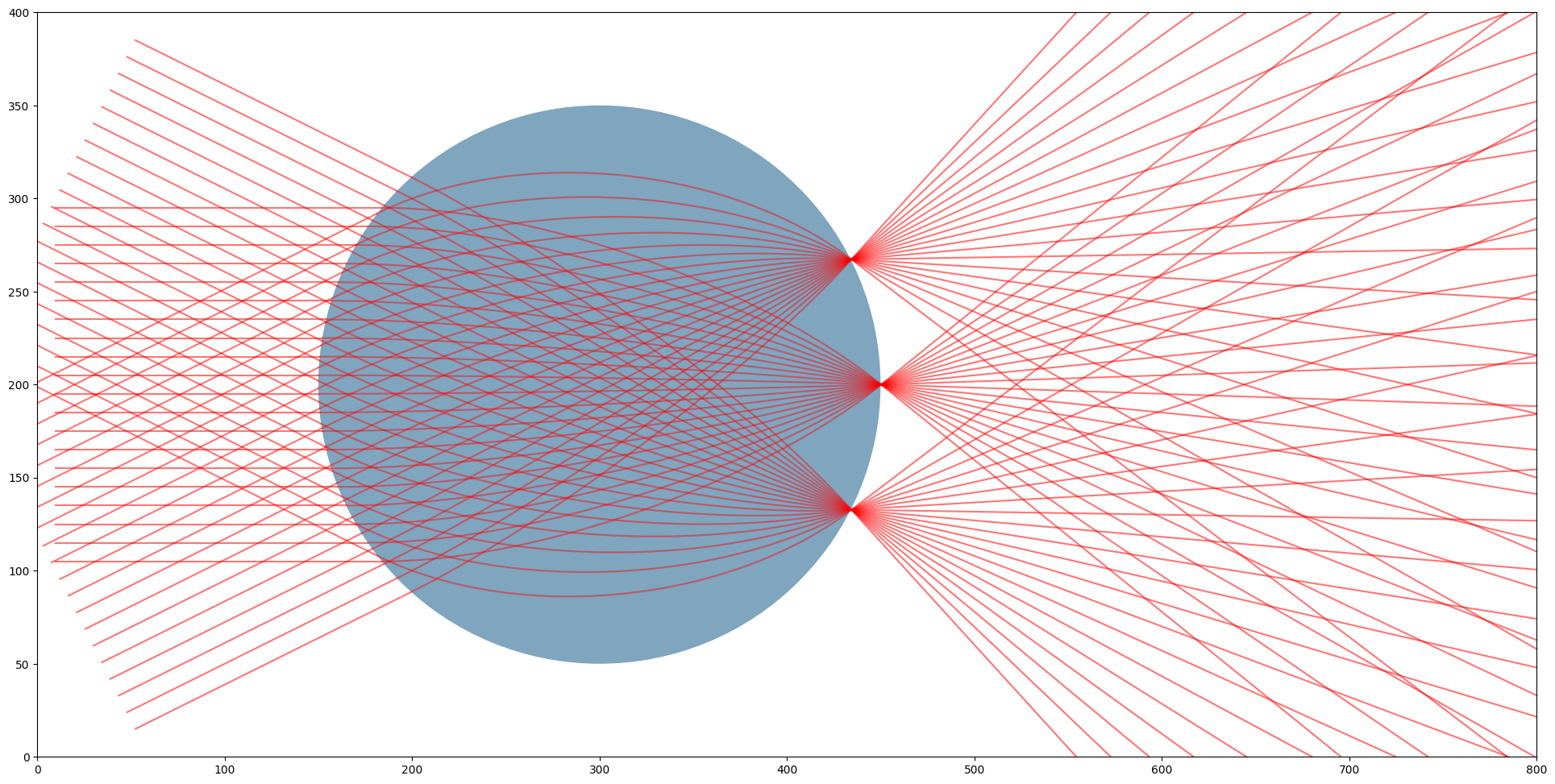Parallel rays going through a Luneburg lens with coefficient p=2 showcasing the peculiar convergence of parallel rays.
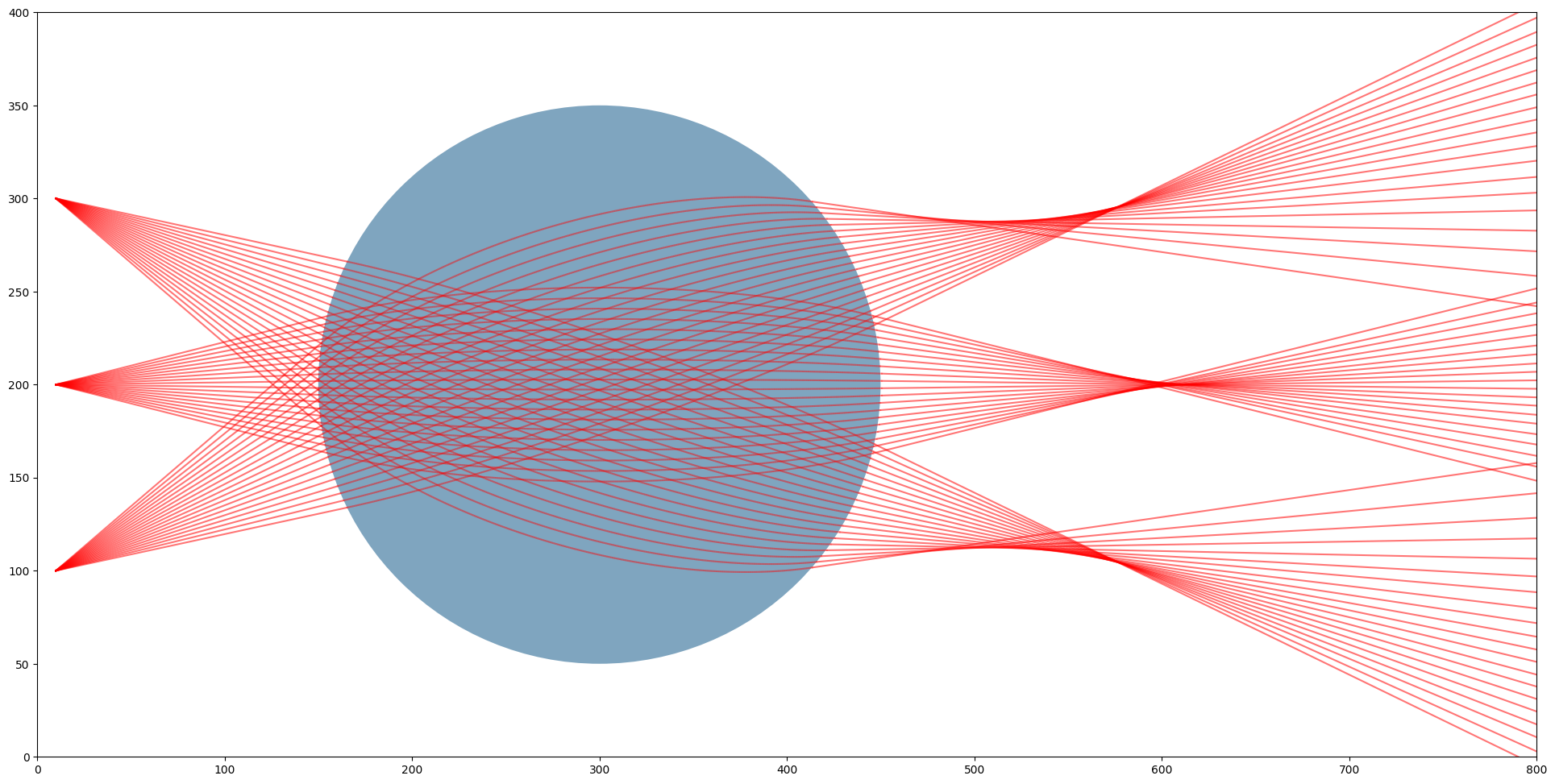For non-parallel rays, the same behaviour no longer holds.